توضیحات
محصول روش نیومارک برای تحلیل سازههای چند درجه آزادی در متلب حاوی بیش از 100 دقیقه آموزش ویدیویی میباشد که از مفاهیم پایه دینامیک سازه شروع شده و در نهایت صحت سنجی یک مقاله معتبر انجام میشود. در این آموزش یک قاب برشی 10 طبقه مورد توجه بوده است و این سازه معیار تحت زلزله السنترو تحلیل میشود و تاریخچه زمانی جابجایی هر یک از طبقات بدست میآید. سپس نتایج حاصل از دستورات با نتایج مقاله مقایسه میشود. این دوره به دانشجویان کارشناسی ارشد مهندسی عمران علی الخصوص دانشجویان گرایشهای سازه و زلزله توصیه میشود. دانشجویان پس از گذراندن این دوره، درک درستی از روابط روش نیومارک خواهند داشت و همچنین قادر خواهند بود، روش نیومارک را به صورت شتاب ثابت یا شتاب خطی برای ساختمانهای برشی اجرا نمایید.
جلسه اول آموزش روش نیومارک برای تحلیل سازه های چند درجه آزادی را رایگان مشاهده کنید!
نتایج دوره آموزشی
1- تاریخچه زمانی جابجایی طبقات
پس از تحلیل سازه در نرم افزار MATLAB به سادگی میتوان تاریخچه زمانی جابجایی را برای تمامی سقفها رسم کرد. این شکل جابجایی طبقه دهم را در زمانهای مختلف نشان میدهد.
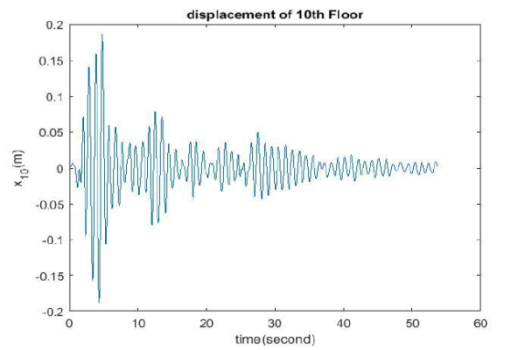
2- ماکزیمم جابجایی طبقات
در مقالات و یا پایان نامهها نیاز است ماکزیمم جابجایی طبقات گزارش شود که پس از تحلیل سازه این نتایج را میتوان به سادگی استخراج نمود.
آشنایی با روش نیومارک
در دینامیک سازهها با معادله حرکت سیستم یک یا چند درجه آزادی آشنا شدیم که به صورت زیر تعریف میشود:
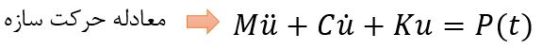
حل این معادله را در دینامیک سازه ما یاد گرفتیم. ولی وقتی بار وارد بر سازه پیچیده باشد یا به عبارتی نتوانیم یک رابطه مشخص برحسب زمان برای آن بار تعریف کنیم، بایستی از روشهای عددی برای حل این معادله استفاده کنیم.
روشهای عددی انواع مختلفی دارد که یکی از معروف ترین آنها روش حل عددی نیومارک میباشد.
در روش نیومارک از دو فرمول اساسی زیر استفاده میشود:
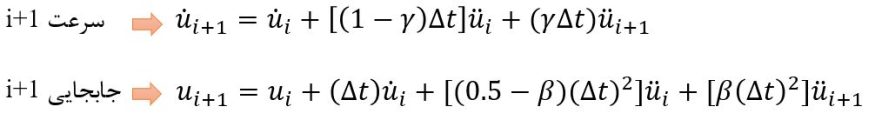
دو تا پارامتر γ و β که در این روابط مشاهده میکنیم، بیان کنندهی تغییرات شتاب بر یک گام زمانی هستند که دقت و پایداری روش را مشخص میکنند. در این روابط γ=1/2 و β بین 1/6 تا 1/4 میتواند مقدار داشته باشد. ما معمولا دو مقدار خاص را برای β مورد بررسی قرار میدهیم که معرف حالت شتاب ثابت و شتاب خطی هستند. در صورتی که γ=1/2 و β=1/4 باشد، شتاب ثابت است و در صورتی که γ=1/2 و β=1/6 باشد شتاب خطی میباشد.
اگر به روابط دقت شود، ما برای محاسبه تغییرمکان و سرعت i+1 نیاز به شتاب i+1 داریم در صورتی که شتاب i+1 را هنوز بدست نیاوردیم. از این رو برای حل این معادله نیاز به سعی و خطا هست.
در دینامیک سازه چوپرا روشی پیشنهاد شده است که نیاز به شتاب i+1 در آن نیست و حل این معادله را برای سیستمهای خطی بسیار آسان کرده است.
روابط غیر تکراری
برای جلوگیری از تکرار، روابط نیومارک را با پارامترهای تعریف شده زیر اصلاح می کنیم:
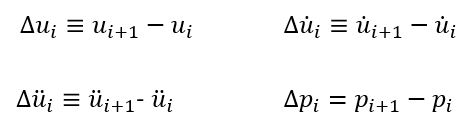
روابط روش نیومارک را میتوان به صورت زیر اصلاح کرد:
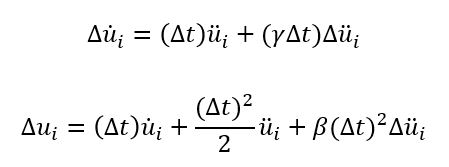
در ادامه باید روابط مربوط تغییرات شتاب و سرعت را از روابط بالا استخراج کنیم. روابط به صورت زیر بدست میآیند:
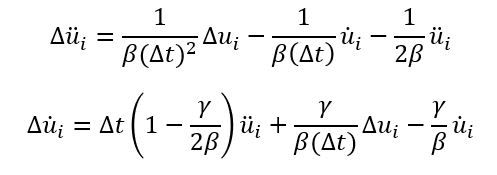
حال روابط بدست آمده در معادله حرکت سازه که بصورت زیر اصلاح شده است، قرار داده میشود:
و در نهایت خواهیم داشت:
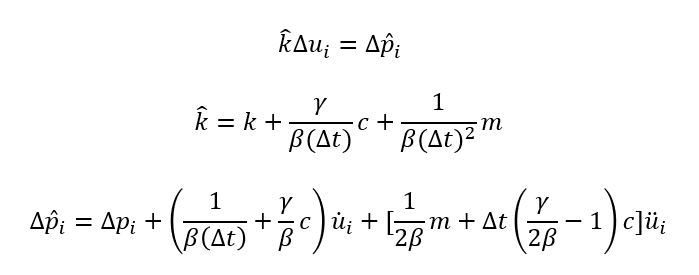
طبق این روابط میتوان روش نیومارک را بصورت شتاب ثابت و شتاب خطی برای سازههای یک درجه و یا چند درجه آزادی پیاده سازی نمود.
مدرس

مهندس جواد قلی زاده
مهندس جواد قلی زاده دانشجوی کارشناسی ارشد مهندسی عمران-زلزله از دانشگاه خوارزمی تهران هستند. از علایق پژوهشی ایشان میتوان به سیستمهای کنترل سازه و بهینه سازی با الگوریتمهای فراابتکاری اشاره کرد.


فاطمه خریدار تایید شده –
من خودم تا حدودی بلد بودم اما موقع اجرا خطا میداد که با این آموزش تونستم ایرادتم را برطرف کنم. خیلی ممنون
حسین –
بسیار عالی بود. ممنونم