روش‌های عددی برای تحلیل دینامیکی سازه‌های تک درجه آزادی

روش‌های عددی را در اینجا توضیح بده و خلاصه ای از مطالبی که در این صفحه صحبت می‌شود. در این صفحه روش‌های عددی تفاضل مرکزی و نیومارک شرح داده می‌شود.

چرا از روش‌های عددی استفاده می‌کنیم؟

اگر نیروی موثر و یا شتاب زمین وارد بر سازه تابع دلخواهی از زمان باشد، حل تحلیلی معادلات حرکت سیستم یک درجه آزادی معمولا غیر ممکن است. برای حل معادلات دیفرانسیل حاکم بر چنین سیستم‌هایی می‌توان از روش‌های عددی گام به گام زمانی استفاده کرد.

روش تفاضل مرکزی (central difference method)

در این روش Δt ثابت است. سرعت از روی جابجایی بدست می‌آید و شتاب نیز با فرض تغییرات خطی از روی سرعت حاصل می‌شود.

می‌توان روش تفاضل مرکزی را بصورت الگوریتم زیر نوشت:

گام اول: محاسبات و مقدار دهی اولیه

میتوان u_-1 را بصورت زیر محاسبه کرد:

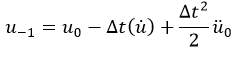
پارامتر k-hat را بصورت زیر تعریف می‌کنیم

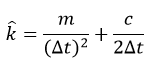
پارامترهای a و b بصورت زیر تعریف می‌شوند:

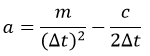
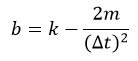
گام دوم: محاسبات برای گام زمانی i

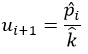
گام سوم: محاسبات برای گام بعدی

i را با i+1 تعویض کرده و گام دوم را تکرار می‌کنیم.

نکته: بطور متعارف برای حصول نتایج با دقت قابل قبول، Δt/T_n<0.1 در نظر گرفته می‌شود.

روش نیومارک

نیومارک در سال 1989 خانواده‎‌ای از روش‌های گام به گام زمانی را برپایه روابط زیر بسط داد:

مقادیر متعارف γ و β بصورت زیر اگر باشد، منجر به نتایج رضایت بخشی می‌شود:

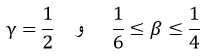
این پارامترها تغییرات شتاب را در یک گام زمانی تعریف می‌کنند و مشخصه پایداری و دقت روش می‌باشند.

طبق کتاب دینامیک سازه رابطه زیر را داریم:

با ترکیب این رابطه با روابط بالایی، پایه‌ای برای محاسبه جابجایی، سرعت و شتاب را در لحظه i+1 بر حسب جابجایی، سرعت و شتاب لحظه i که معلوم هستند، به وجود می‌آید. در روابط نیومارک چون به شتاب i+1 نیاز است، نیاز به تکرار روش هست. برای سیستم‌های خطی طبق کتاب دینامیک سازه چوپرا، معادلات روش نیومارک را می‌توان طوری اصلاح نمود که نیاز به تکرار نباشد.

برای دریافت دستورات متلب روش نیومارک برای تحلیل سازه‌های چند درجه آزادی کلیک کنید.